本经验通过函数的定义域、单调性、凸凹性等性质，介绍函数用导数工具画函数y=arctan(ax+b/cx-d)的图像的主要步骤。
分式函数，形如f(x)=p(x)/q(x) 的函数叫做分式函数，其中p(x)、q(x)是既约整式且 q（x)的次数不低于一次，且q(x）必须满足不等于0。
在利用导数讨论函数的单调区间时，首先要确定函数的定义域，解决问题的过程中只能在定义域内，通过讨论导数的符号来判断函数的单调区间。
计算函数的二阶导数，得到函数的拐点，根据拐点的符号，判断函数的凸凹性，并解析函数的凸凹区间。
解析函数的五点图，根据函数的定义域，结合函数的单调性和凸凹性，列举函数上的部分特征点，并以五点图表表示。
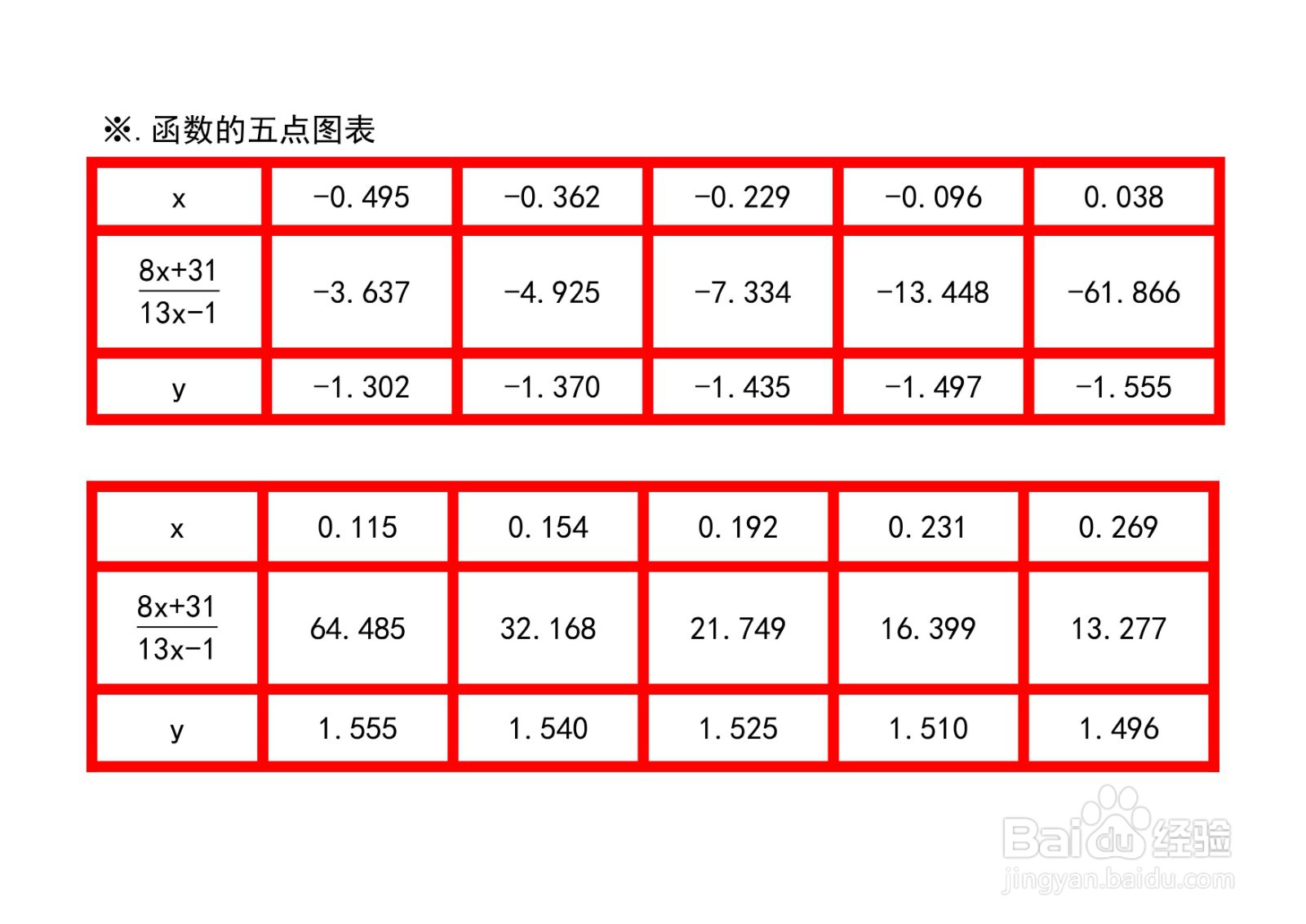
综合以上函数的定义域、单调性、凸凹性、奇偶性等性质，解析函数的图像示意图如下。
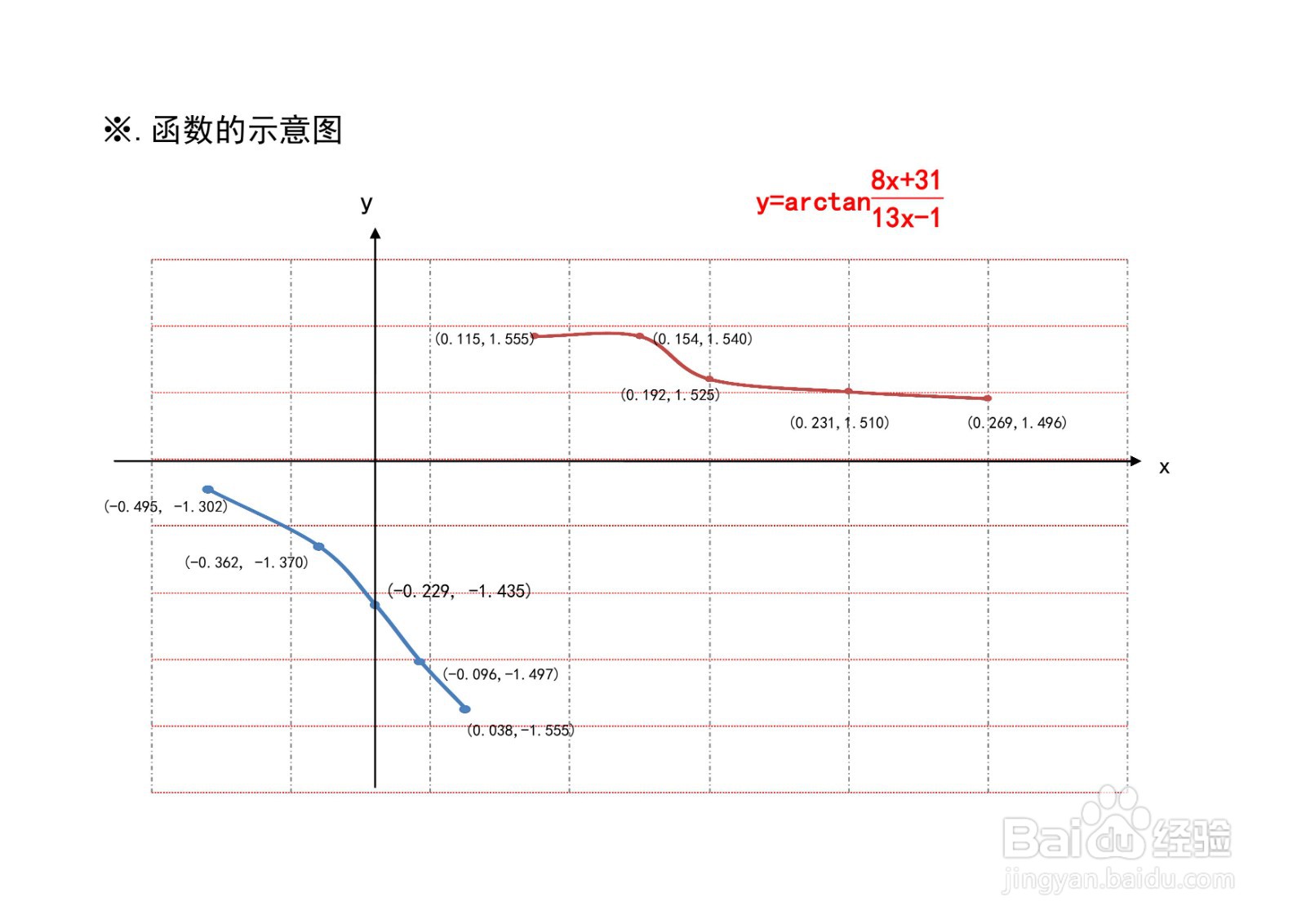END未经允许不得转载：经验百科 » 函数y=arctan(ax+b/cx-d)图像性质应用举例之14
推荐给朋友的视频，可在主页推荐列表中查看。下面将介绍抖音APP如何查看推荐给朋友的视频。工具/原料vivox80OriginOS 3.0抖音27.7方法/步骤进入抖音APP首页，点击底部“我”选...
阅读(0)评论(0)
别人夸你帅怎么幽默回答方法/步骤1、幽默一点 首先，最机智的回复就是幽默一点的回复，以调侃的方式回复，比如我们可以回复“我就喜欢你这样一本正经胡说八道的人”，这种调侃的...
阅读(0)评论(0)
如下：1、隔窗闻漫雪，咫尺若天涯。2、真情到久难相见，相约梦中总是缘，千杯万盏终恨少，不觉梦醒晓风寒。3、众里寻他千百度，蓦然回首，那人却在，灯火阑珊处。4、既然不能在一起，生命为什...
阅读(0)评论(0)
关闭个性化推荐功能，即可关闭直播推荐，下面将介绍具体的设置方法。工具/原料小米13MIUI14.0汽水音乐7.8.0方法/步骤打开APP我的页，点击右上角“设置”图标。进入设置页，点击“隐...
阅读(0)评论(0)
对方说上班了，怎么回消息 方法/步骤首先对方和你说上班了，第一个意思是告诉你他的状态在忙，这时候你可以表示理解说：你先忙着，我就不打扰你啦。这可以表达出你的体贴，还很善解人意...
阅读(0)评论(0)
如果男生给你说七夕节快乐该怎么回答呢？方法/步骤假如你是一个女生，一个男生给你说七夕节快乐的话。那么他可能是想看看你有没有男朋友呢？假如你已经有了对象他给你发的话，那么...
阅读(0)评论(0)
下面将介绍快手极速版静音模式怎么设置。工具/原料红米Note12MIUI14.0快手极速版11.9.40方法/步骤打开快手极速版app，在个人主页点击“三个点”图标。在更多页，点击“设置”图...
阅读(0)评论(0)
人家发消息说句七夕快乐，怎么回复对方工具/原料微信，QQ或短信方法/步骤如果对方并不是你喜欢的类型，你可以回答说：嗯，谢谢你，祝福你。如果一个男生给你说七夕快乐，说明他是对你有好...
阅读(0)评论(0)
经验百科
最新评论
好东西